The other day I was interested in drawing a fairly simple nuclear reaction network in$$\LaTeX$$. I thought that tikz would be a good way of doing this. Basically, tikz is a way to generate vector graphics directly inside the $$\LaTeX$$ source code. I figured that somebody would have an example online of how to draw a simple directed graph with annotations on the connections.
There does exist a fairly new package called tkz-graph that is specifically designed for drawing such a graph. Unfortunately, there are some limitations that affected my final image. One thing I wanted to do was color the nodes of the network with different colors to demonstrate different linear chains in the network, but that seems to be difficult with the current version as coloring nodes differently is not currently supported without defining a node type for each style.
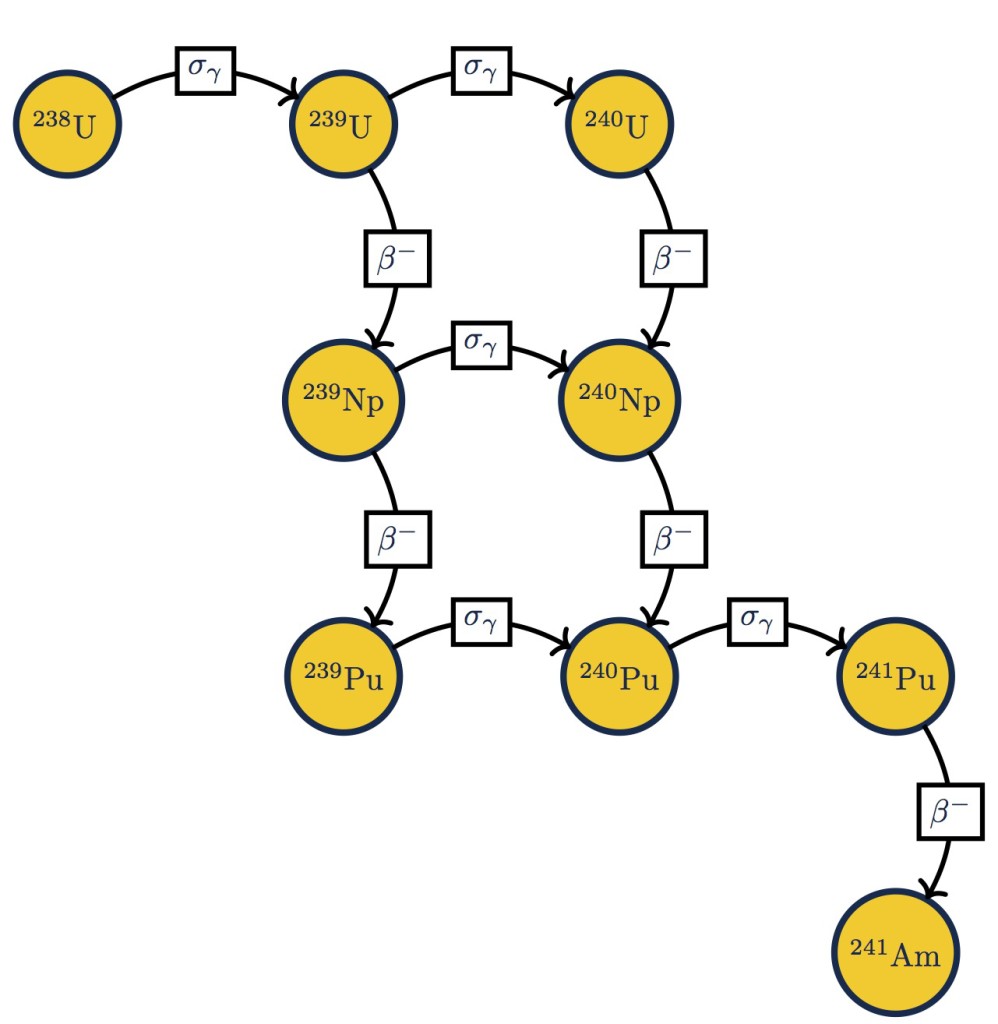
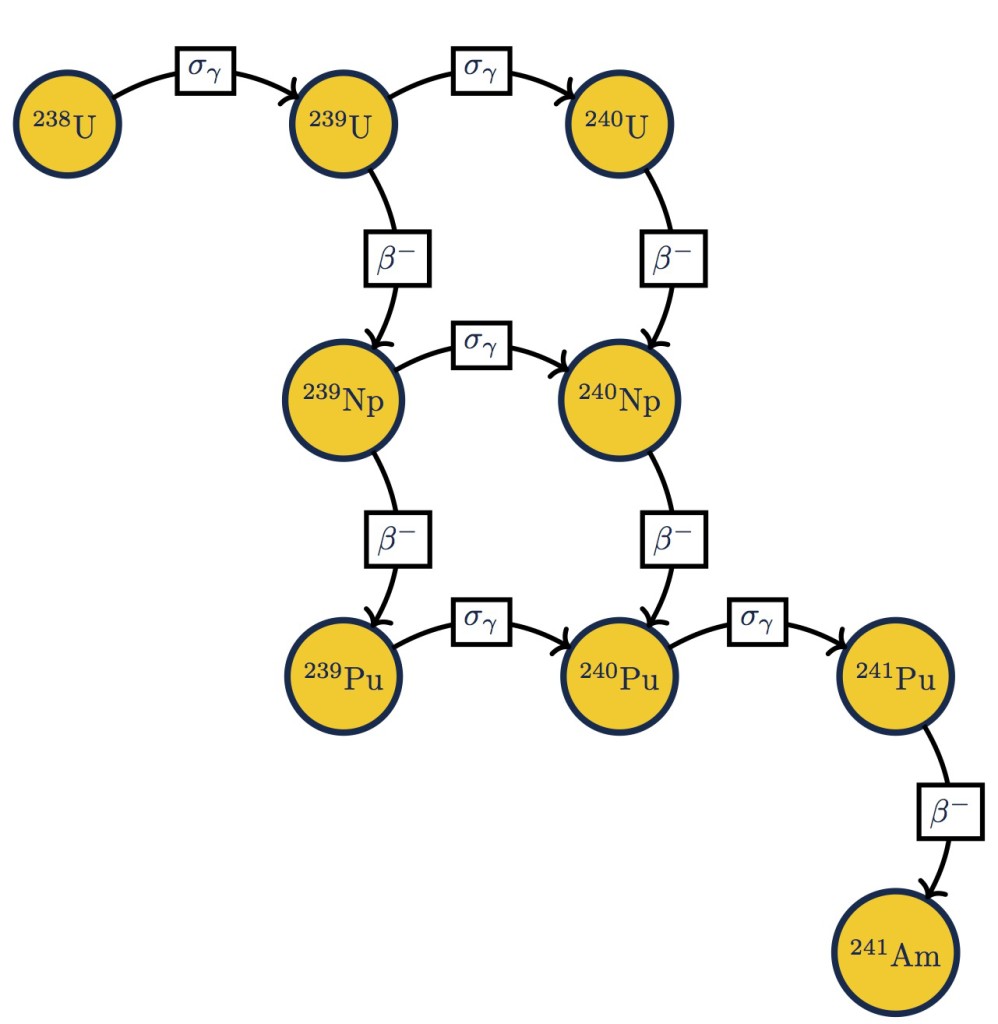
The end result was pretty nice
Transmutation and decay network for uranium-238
This network could be much more involved insofar as there could be higher nuclides plutonium, but the point here is to illustrate how these networks can be draw in $$\LaTeX$$.
The code for this figure is given below, after the jump.
\documentclass{article}
\usepackage{tikz,tkz-graph}
\begin{document}
\definecolor{maize}{HTML}{FFCB05}
\definecolor{theblue}{HTML}{00274C}
\begin{figure}
\SetVertexNormal[Shape = circle,
FillColor = maize,
LineWidth = 2pt]
\SetUpEdge[lw = 1.5pt,
color = black,
labelcolor = white,
labeltext = red,
labelstyle = {draw,text=theblue}]
\tikzset{EdgeStyle/.style={->}}
\tikzset{VertexStyle/.style = {text = theblue, shape=circle, fill=maize, line width=2pt, draw = theblue}}
\begin{center}
\begin{tikzpicture}[scale=1]
\Vertex[Math,L=^{238}\mathrm{U\,},x=0 ,y=7]{U238}
\Vertex[Math,L=^{239}\mathrm{U\,},x=3 ,y=7]{U239}
\Vertex[Math,L=^{240}\mathrm{U\,},x=6 ,y=7]{U240}
\Vertex[Math,L=^{239}\mathrm{Np},x=3 ,y=4]{Np239}
\Vertex[Math,L=^{240}\mathrm{Np},x=6 ,y=4]{Np240}
\Vertex[Math,L=^{239}\mathrm{Pu},x=3 ,y=1]{Pu239}
\Vertex[Math,L=^{240}\mathrm{Pu},x=6 ,y=1]{Pu240}
\Vertex[Math,L=^{241}\mathrm{Pu},x=9 ,y=1]{Pu241}
\Vertex[Math,L=^{241}\mathrm{Am},x=9 ,y=-2]{Am241}
\tikzset{EdgeStyle/.append style = {bend left}}
\Edge[label = $\sigma_\gamma$](U238)(U239)
\Edge[label = $\sigma_\gamma$](U239)(U240)
\Edge[label = $\beta^-$](U239)(Np239)
\Edge[label = $\beta^-$](U240)(Np240)
\Edge[label = $\sigma_\gamma$](Np239)(Np240)
\Edge[label = $\beta^-$](Np239)(Pu239)
\Edge[label = $\beta^-$](Np240)(Pu240)
\Edge[label = $\beta^-$](Pu241)(Am241)
\Edge[label = $\sigma_\gamma$](Pu239)(Pu240)
\Edge[label = $\sigma_\gamma$](Pu240)(Pu241)
\end{tikzpicture}
\end{center}
\caption{A transmutation network for $^{238}$U.}\label{fig:full_u238}
\end{figure}
\end{document}
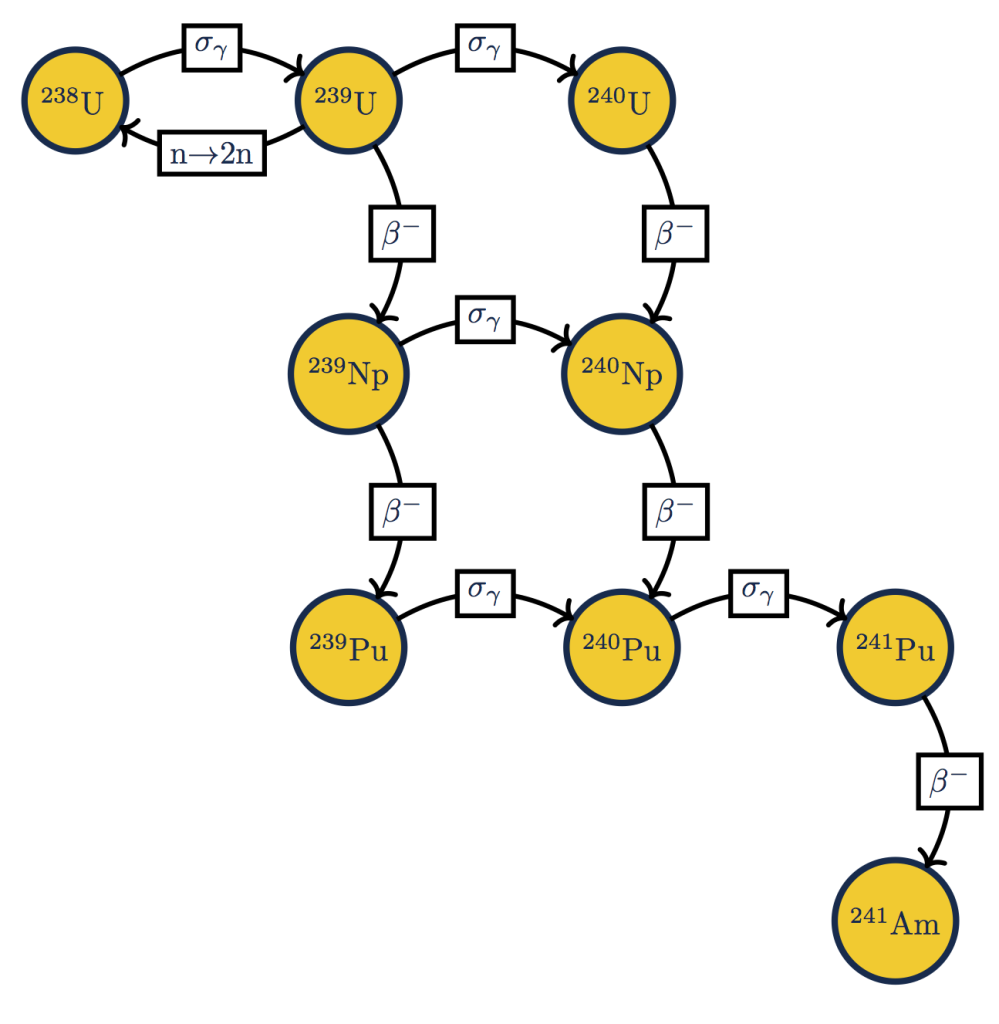
A couple of notes on this figure. The $$\sigma_\gamma$$ connections refer to radiative capture reactions, and the $$\beta^-$$ connections are beta decays of nuclei. There are other reactions that we could represent here, such as $$(n,2n)$$ reactions, here is a figure with a single such reaction
Reaction network with an (n,2n) reaction
