The special issue of Nuclear Science and Engineering featuring papers from the 2019 Mathematics and Computation Meeting held in Portland is now available. I was the guest editor for this issue.
You can read my introduction to the issue, and find all of the papers at this link: https://www.tandfonline.com/doi/full/10.1080/00295639.2020.1802915
Thanks to all of the contributors to the issue.
Reed’s problem [1] is a common test problem for transport codes. It is comprised of heterogeneous materials with strong absorber, vacuum, and scattering regions. These regions are valuable to testing different aspects of numerical discretizations. For instance, the vacuum region is troublesome for second-order forms of the transport equation.
Jim Warsa published solutions obtained from eigenfunctions expansions for Reed’s problem in 2002 [2]. The are in the form of exponentials and hyperbolic trig functions and have several terms that must be added together carefully to avoid numerical instability.
I have written a Mathematica notebook to evaluate the solutions that you can download here. Or, if you just want the solutions, you can download a CSV of them here. The solution is also plotted here.
[1] Reed, William H. “New difference schemes for the neutron transport equation.” Nuclear Science and Engineering 46.2 (1971): 309-314.
[2] Warsa, J. (2002). Analytical SN solutions in heterogeneous slabs using symbolic algebra computer programs. Annals of Nuclear Energy, 29(7), 851–874.
When material is moving, the physics of radiative transfer changes to account for Doppler shifts in the frequency, and the motion of the material causes the opacities to need to be evaluated at different energies. This complication has been studied for a long time, but accurate numerical methods (and their implementation is a bit of a challenge).
One common locus of argument is how important these corrections are when the material is moving slow relative to the speed of light. Many of the correction terms appear to be small when the material speed is much smaller than the speed of light.
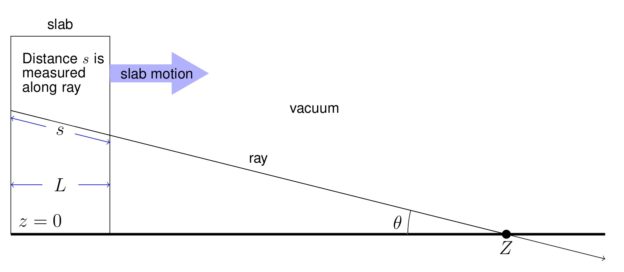
In a recent extended summary for the 2021 M&C Meeting, Nick Gentile and I developed some benchmark solutions for the spectrum of light that would be measured in front of a moving slab. We show that, even at a speed of 5% the speed of light, the spectrum one measures is significantly different when one either ignores the material motion corrections or leaves of some seemingly unimportant terms. Moreover, the errors that result from ignoring these terms get worse as the spectrum resolution is increased. See the full document here.
The Mathematica notebooks used to produce the benchmarks can be found on Github.
Consider a plane of thickness $$\Delta z$$. The plane emits $$q$$ neutrons per second per unit area at a single energy and is comprised of a pure absorber. What is the angular flux at the right edge of the plane, $$\Phi(\Delta z, \mu)$$? Use your solution to give the angular flux emerging from an infinitely thin plane source. Hint: Use an integrating factor of $$\exp{(\sigma z / \mu)}$$.
The derivation of this solution is after the jump