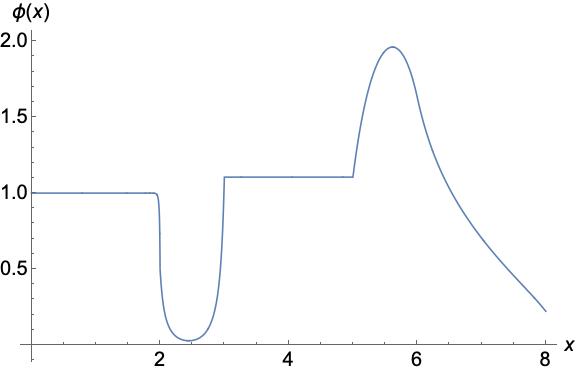
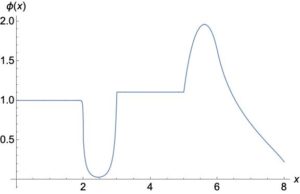
Reed’s problem [1] is a common test problem for transport codes. It is comprised of heterogeneous materials with  strong absorber, vacuum, and scattering regions.  These regions are valuable to testing different aspects of numerical discretizations.  For instance, the vacuum region is troublesome for second-order forms of the transport equation.

Jim Warsa published solutions obtained from eigenfunctions expansions for Reed’s problem in 2002 [2].  The are in the form of exponentials and hyperbolic trig functions and have several terms that must be added together carefully to avoid numerical instability.

I have written a Mathematica notebook to evaluate the solutions that you can download here. Or, if you just want the solutions, you can download a CSV of them here. The solution is also plotted here.

[1] Reed, William H. “New difference schemes for the neutron transport equation.” Nuclear Science and Engineering 46.2 (1971): 309-314.

[2]  Warsa, J. (2002). Analytical SN solutions in heterogeneous slabs using symbolic algebra computer programs. Annals of Nuclear Energy, 29(7), 851–874.